Formule per trovare Vertici, Fuochi, eccentricità e assi dell'ellisse (asse maggiore, asse minore e asse focale) Come tracciare il grafico dell'ellisse. Punti di intersezione tra retta ed ellisse. Posizioni reciproche tra retta ed ellisse. Condizione di appartenenza di un punto ad un'ellisse (Ellisse passante per un punto). Come ricavare l'equazione dell'ellisse che passa per due punti di cui si conoscono le coordinate. Impostazione del sistema, risoluzione dello stesso tramite.
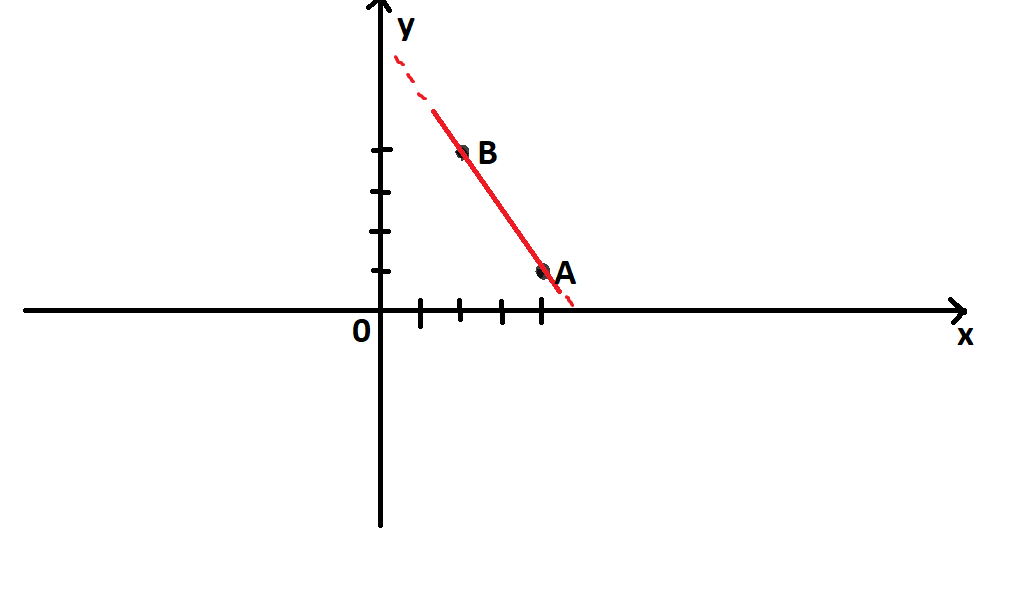
L'Equazione di una retta passante per due punti Blog didattico

Proiezioni ortogonali ELLISSE costruzione per 8 punti

Equazione di una retta per due punti. Matematica terza media

Equazione dell'ellisse con centro nell'origine YouTube

Come ricavare l'equazione di un'ellisse Esercizi svolti YouTube

Equazione di una Circonferenza dati 2 Punti e la Retta su cui giace il Centro (Metodo Analitico
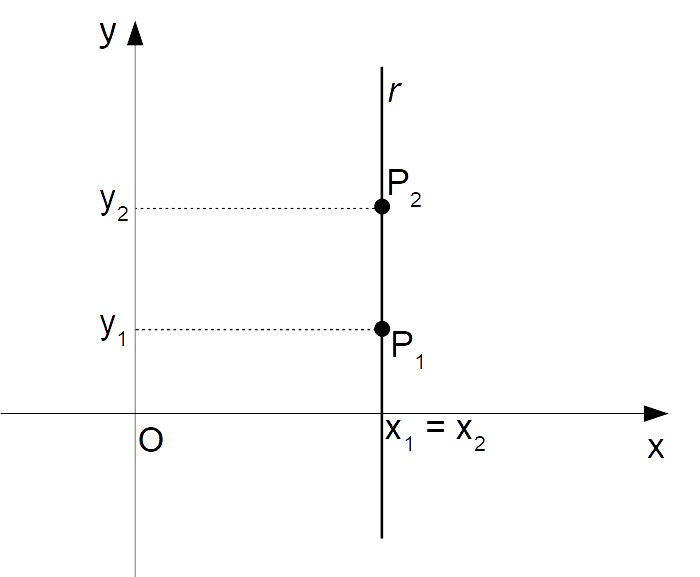
Retta passante per due punti SìMatematica
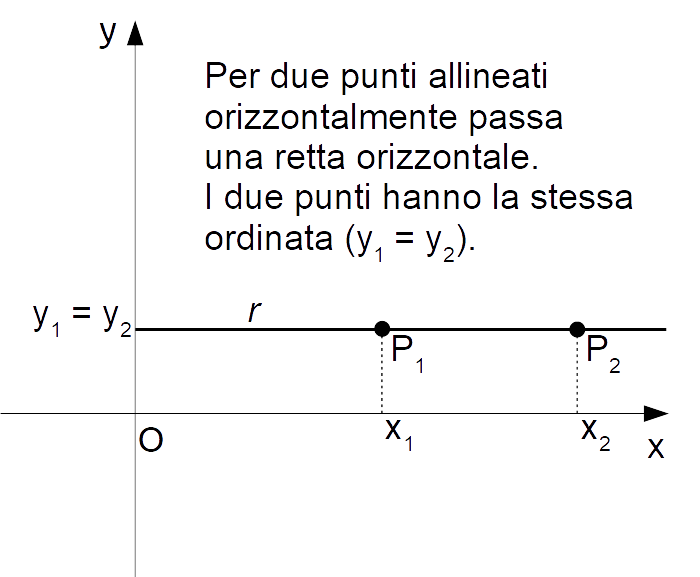
Retta passante per due punti SìMatematica

Equazione della retta passante per due punti 📐 YouTube

Retta tangente ellisse Studenti.it

Ellisse passante per due punti, esercizi di geometria analitica YouTube
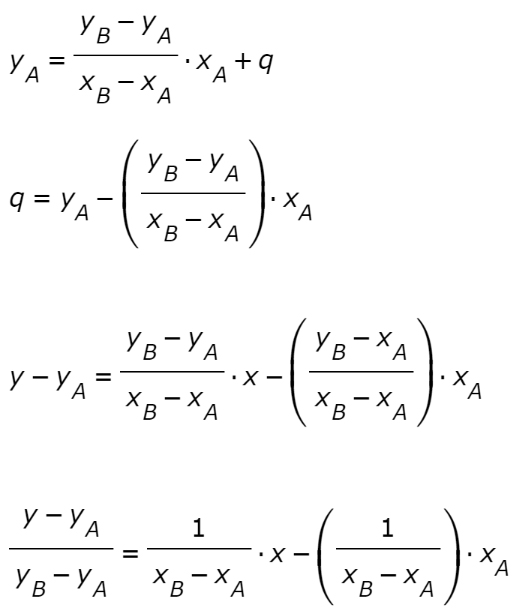
Equazione Del Piano Passante Per Un Punto brahays
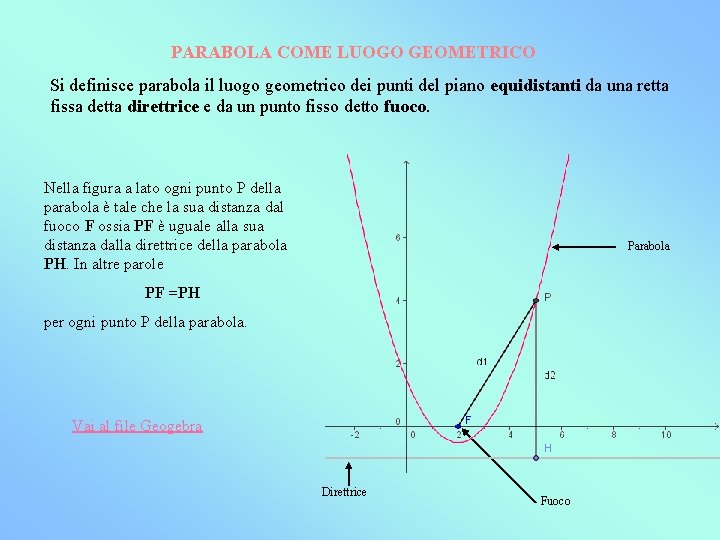
LA PARABOLA PREREQUISITI DISTANZA TRA DUE PUNTI Si

La retta passante per uno e due punti Andrea il Matematico

Circonferenza per tre punti metodo degli assi Andrea il Matematico

Ellisse e retta per Superiori Redooc

Retta passante per due punti e suo coeff. angolare YouTube

📐💻 Equazione di una retta passante per due punti guida pratica con esempi e formule YouTube

Proiezioni ortogonali ELLISSE costruzione per 8 punti

PPT L’ ELLISSE PowerPoint Presentation, free download ID674448
Di conseguenza, la relazione che lega a, b, e c sarà: c2 = a2 - b2. Sostituendo a c le coordinate del fuoco, avremo: 12 = a2 - b2. 1 = a2 - b2. Sappiamo, inoltre che l'ellisse passa per il punto. P (1; 1). In questo punto, l'equazione dell'ellisse assume i seguenti valori: Calcoliamo il minimo comune denominatore a primo membro:. Quando l'ellisse passa per il punto P2 , poiché. x = 2. y = 3. l'equazione assume i seguenti valori: α· (2)2 + β· (3)2 = 1. 4α + 9β = 1. Ora, per trovare i valori di α e di β risolviamo un sistema formato dalle due equazioni scritte: Ricaviamo α dalla prima equazione e la sostituiamo nella seconda: